In this lecture we will learn about electric potential, and electric potential difference, which is also known as voltage.
You can watch the following video or read the written tutorial below the video.
Electric Potential
In the previous lecture, we’ve talked about electric potential energy which is dependent upon the charge of the object experiencing the electric field. Now, we’re going to learn about electric potential, which is only dependent upon the position of the object.
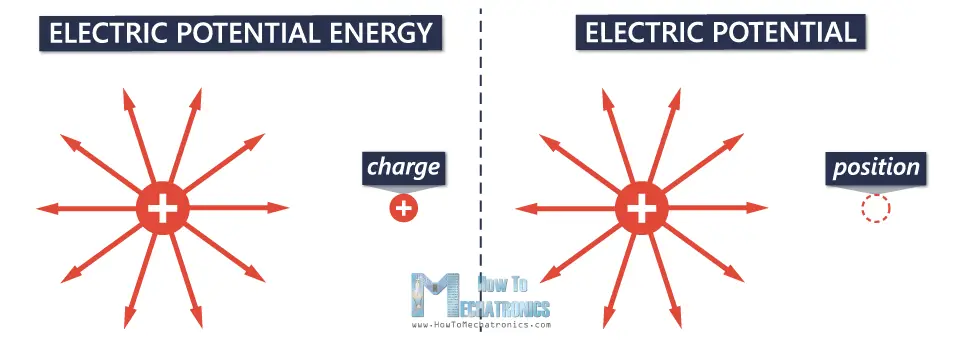
Electric potential (or just potential), is simply a measure of the electric potential energy per unit of charge.
Electric Potential Formula
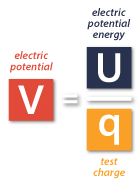
This is the basic equation for calculating the electric potential, which shows that the electric potential V is equal to the electric potential energy U, divided by the charge q that would be placed at a point some distance away from the main charge.

The electric potential energy U is equal to the Coulomb’s constant k, multiplied by the charge that creates the potential big Q, times the charge that would be placed at a point some distance away from the main charge small q, and divided by that distance r.
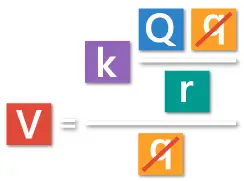
In order to calculate the electric potential, we just need to divide the potential energy with small q.
We can notice that small q appears twice in the equation, so we can cancel it out.

Now we have this simple equation.
The equation shows that the potential is directly proportional to the amount of charge Q – as the charge increases, the potential increases, and opposite, as the charge decreases, the potential decreases.
On the other side, it is inversely proportional to the distance r, because as you move away from the charge, the potential is going to decrease, and as you move closer to the charge, the potential is going to increase.
Finally, we would get an amount of electric potential energy that each unit of charge would have at that point.
Related: Coulomb’s Law
Unit of Electric Potential
Now let’s go back to the basic equation.

We know that electric potential energy is measured in Joules, and the unit of charge is Coulomb. So, the unit of measurement for electric potential is Joules per Coulomb, or in one word Volts.
Example for Electric Potential

There’s a point charge equal to +2 µC, and we want to find the electric potential 15 cm (0.15 m) away from that charge.
Now, we can use the equation in order to calculate the electric potential.
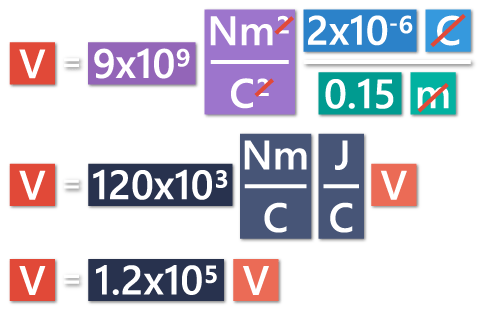
We got a positive electric potential of +1.2×105 V.
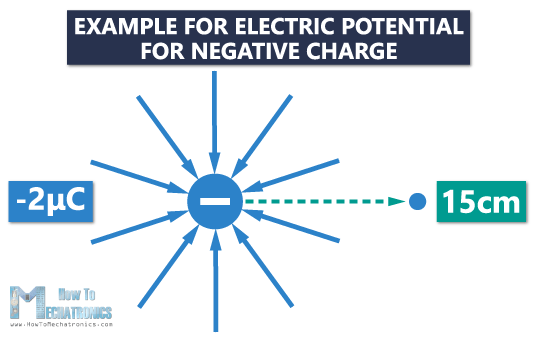
In case we had a negative charge, let’s say -2 µC, the electric potential at that same point would be -1.2×105 V. We would get the same value, but with the minus sign.
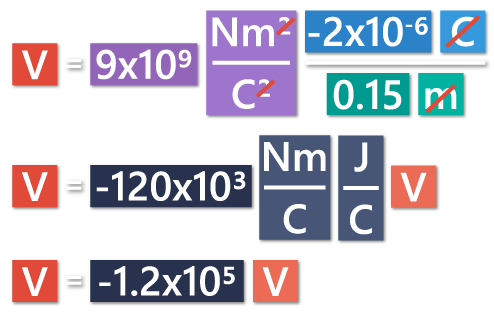
Graph of Electric Potential
Let’s take a look at this graph of electric potential. The X axis shows the distance away from the charge, while the Y axis shows the electric potential at a certain point.
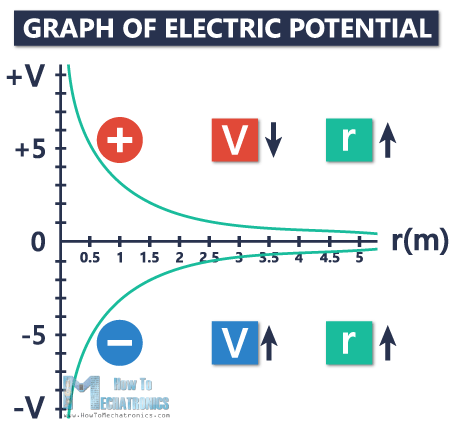
Here we have a positive charge, and the potential around a positive charge is always positive. As you move away from the charge, as the distance from the charge increases, the potential becomes less positive, and decreases getting closer and closer to zero.
On the other side, we have a negative charge, and the potential around a negative charge is always negative. As you move away from the charge, as the distance from the charge increases, the potential becomes less negative, and actually increases, also getting closer and closer to zero.
If you’re infinitely far away from the charge, the potential is going to be zero for both positive and negative charges.
Related: What is Electric Charge and How Electricity Works
Electric Potential Difference (Voltage)
Now we can move on to the electric potential difference, or voltage.
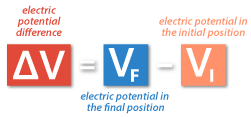
By definition, the electric potential difference, or voltage, is the difference in electric potential between the final and the initial position when work is done upon a charge to change its potential energy.
Example for Electric Potential Difference (Voltage)
Now, let’s look at an example which will help us easily understand the term voltage.

We have a positive charge of +1.6×10-19 C. It is the main charge that is creating the potential.
The first circle is the first energy level, at a distance of 2.5×10-11 m away from the charge. The second circle is the second energy level, at a distance of 4.2×10-12 m away from the charge.
In order to find the electric potential difference, or voltage, we need to find the potential at the point A and the potential at the point B.
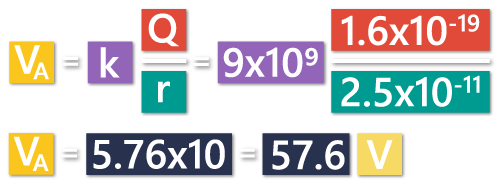
The potential at the point A, which is the first energy level is going to be 57.6 V.
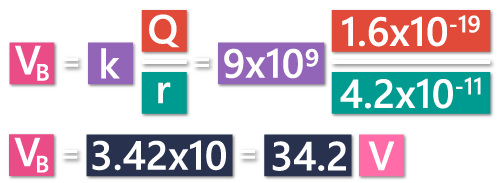
The potential at the point B, which is at a greater distance, is going to be 34.2 V.
First, we’re going to calculate the voltage as we move from A to B, and then from B to A.
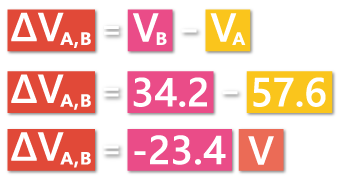
In the first case, A is our initial potential, and B is our final potential. So, the potential difference is going to be final minus initial potential, or 34.2–57.6 =-23.4 V. We got a negative potential, which means as we go from A to B the potential decreases.
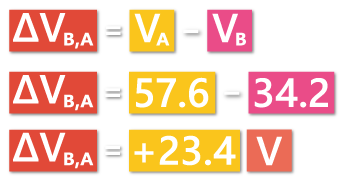
In the second case, B is our initial potential, and A is our final potential. So, the potential difference is going to be 57.6-34.2=+23.4 V. We have a positive potential, or as we go from B to A the potential increases.
What does that mean?
As we go from A to B, the electric potential decreases due to the fact that we have a positive main charge, and its electric field lines point outwards. If we place a positive test charge in the first energy level, the electric potential energy will be larger. The point charge will repel the test charge, because the density of the electric field lines is much stronger. In B, the density of the electric field lines is weaker, and the electric potential energy is smaller.
That’s all for electric potential and electric potential difference. I hope it was helpful and you learned something new.