Work and Electric Potential Energy

In this lecture we will learn about work and electric potential energy. You can watch the following video or read the written tutorial below.

Work

In the previous lectures we’ve talked about electric fields and forces, and how they affect the things in their surroundings. If we understand forces, we can easily understand work!

Let’s say, we observe an object, and a force is applied on that object. The force is doing work if the object moves.

But what is work?

Work is a product of the magnitude of the displacement of an object and the component of the force parallel to the displacement.

Work is a scalar quantity defined only by its magnitude, and it can be positive or negative.

Example for Work

Now, let’s take a look at a simple example that will help you easily understand and calculate work.

Work When Force and Displacement Are Parallel

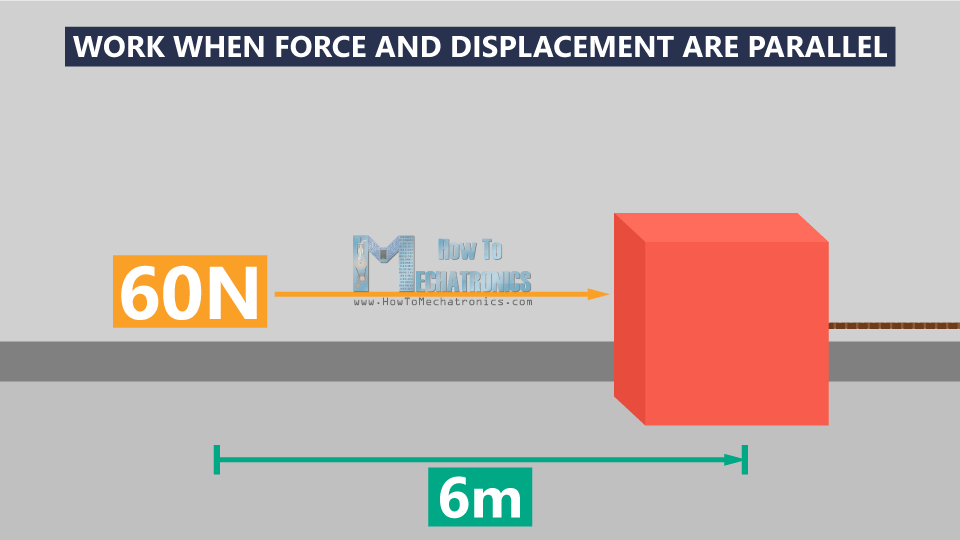
In the first scenario you’re pulling a box with a rope across the floor. The box is the object, and the force you’re using to pull the box is an external force. Let’s say the rope is parallel to the floor, and you’re pulling the box straight behind with a force of 60 Newtons. You’re moving the box 6 meters across the floor, which means you’re doing work on the box. But how much work did you do?

The equation shows that work is equal to the magnitude of the applied force, times the distance we moved the object, times the angle between the force and the displacement θ (theta).

In the example, the force and the displacement are parallel to each other, and in the same direction, the angle between them θ is 0°, and cosθ is 1.

Whenever the force and the displacement are in the same direction, θ=0°.

If you moved the box 6 meters with a constant force of 60 Newtons, you actually did a 360 Newton/meters of work on the box, which is equivalent to 360 Joules. Instead Newton/meters, the work is expressed in units called Joules.

Work When Force and Displacement Are Not Parallel

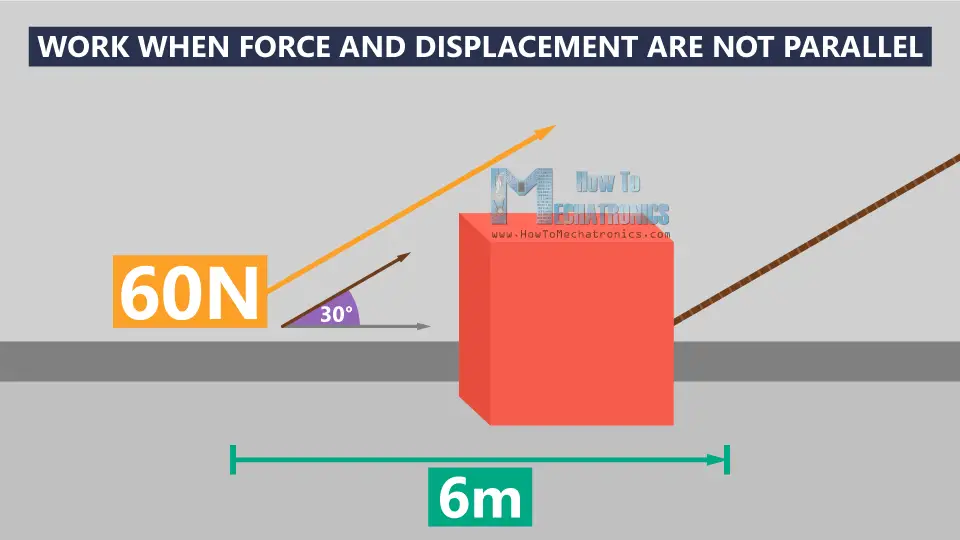
In the second scenario, you’re pulling the box at 6 meters distance, with a constant force of 60 Newtons, but now you’re pulling at an upward angle of 30°, and the box moves parallel to the surface. So, the force you apply to the box is not in the same direction as the direction in which the box is moving. In that case, only the components of the applied force that are parallel to the displacement are part of the work done on the box.

The angle θ here is 30°, and cosθ is 0.866.

Now we have everything we need to calculate the work. We plug everything in and we get 311 Joules, which is less work in this case.

Work When Force is Applied without Displacement of the Object

In the third scenario, you push a wall with a force of 60 Newtons. You may feel that you’re doing a lot of work, but the wall won’t move, so you’ve done zero work. This means that work can only be done when displacement occurs.

Work When the Magnitude of the Force Varies

What if the magnitude of the force varies? For example you started pulling harder, but you got tired and the force got smaller the farther you dragged the box. In this case, to find the work, you need to calculate the force you applied by using integration. And this is the equation that will help you calculate the work:

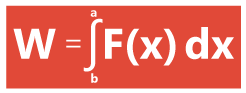
The same principle that we explained so far in this video applies to charges as well!

Energy

We already said that work is measured in Joules. But, Joules are also used as the units for energy, because work is just a change in energy.

In other words, energy is the ability, or the capacity to do work.

There are different kinds of energy, but in this lecture we will pay attention to potential energy.

Potential energy is energy that could be used to do work.

It is energy due to position. And the object needs to be positioned where we can get that energy back out again. Potential energy is denoted by capital U.

Gravitational Potential Energy

There’s a gravitational potential energy, stored in an object as the result of its vertical position or height.

If you hold a book 1.5 meters above the ground, we can say that the book has gravitational potential energy. You have added energy to the book by lifting it up, or in other words, you have done a work on that book. And if you let it go, gravity will exert a force, and the book will fall down to the ground.

When the book is on the ground it has zero gravitational potential energy, because gravity can’t do work on it anymore.

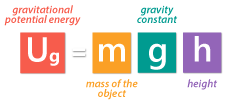
We can calculate gravitational potential energy by multiplying the mass of the book times the constant for gravity times the height of the book.

For example, the mass of the book is 0.5 kilograms, and you’re holding it 1.5 meters above the ground, the gravitational potential energy will be 7.35 Joules.

This can only work if we’re using conservative forces.

A conservative force is a force where the work that we’re putting into the object is independent of the path which that object takes. The object needs to be positioned where we can get that energy back out again.

But what if I just take the book, and drag it across the floor? In that case, the book doesn’t have a potential energy, because it is not going to move back to its initial position.

This means that if you just add a force over a given distance, if you do work on an object, it doesn’t mean that the object will have a potential energy.

Electric Potential Energy

We also have conservative forces when we’re looking at charges. In a gravitational field we have a mass that has a gravitational potential energy, and on the other side, in an electric field, we have charges that have an electric potential energy.

The electric potential energy describes how much stored energy a charge has, when moved by an electrostatic force.

We can calculate the potential energy only if we determine a reference point. The reference point is always arbitrary.

Example for Electric Potential Energy

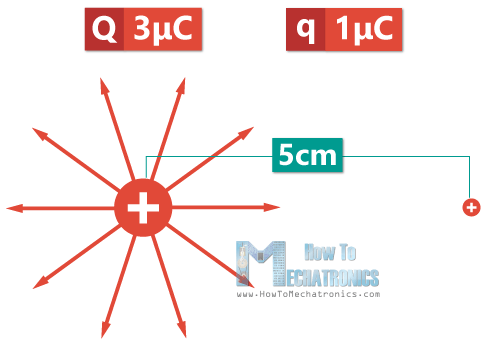
Let’s say we have a system of two positive charges: a point charge Q equal to 3 μC, and a test charge, q equal to 1 μC. The test charge is 5 cm away from the point charge. Q generates an electric field with the electric field lines pointing outward. This means that if we bring the test charge closer to the point charge it would be repelled.

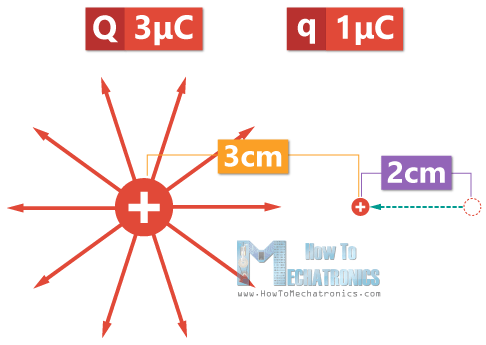
Now, let’s say we want to bring the test charge closer, at 3 cm distance from the point charge. That would mean moving the test charge 2 cm against the direction of the electric field, which would require work by an external force.

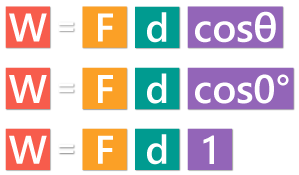
The angle θ in this case is 0, and cosθ is 1.

Instead F, we will use the equation for electric force, and instead d, we will use r for the distance. R cancels out, and we’re left with this equation:

We use the same equation to calculate the electric potential energy U!

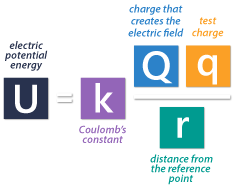
The electric potential energy U is equal to the Coulomb’s constant k, multiplied by the charge that creates the electric field Q, times the charge that would be placed at a reference point some distance away from the main charge q, and divided by the distance from the reference point r.

Now let’s go back to the example, and calculate the electric potential energy:

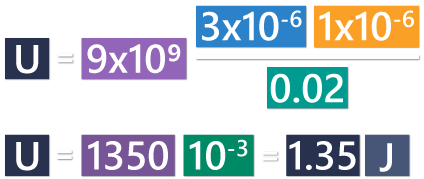
The potential energy at 3 cm distance from the point charge is 1.35 Joules.

Summary

From the equation for electric potential energy, we can notice that the greater the charge on the test charge, the greater the repulsive force, and the more work would have to be done to move it closer to the positive point charge.

Opposite, the movement of a positive test charge in the direction of an electric field would occur without the need of work by an external force. This will further result in losing potential energy.

That would be all for this lecture. I hope it was helpful and you learned something new. In the next Basic Electronics tutorial we will talk about Electric Potential and Electric Potential Difference.