In this lecture we will learn about electric field, the properties of the electric field lines, and the superposition principle. You can watch the following video or read the written tutorial below.
Two electrically charged objects exert a force on each other. They also exert a force on each other even when they are not in contact. This force is called an action at a distance force.
What is an Electric Field?
If we have a charged object we can actually predict what will happen to other electric charges when they are brought close to that object.
A charged object modifies the space around it, forming an electric field. The electric field has an ability to act with a force on another electric charge placed at any point of the field.
When we talked about Coulomb’s Law we observed the force between two charges as an action between two objects, and now we’ll observe the force as an action that the electric field exerts on the charge that enters that field.
Michael Faraday was a British scientists, and was the first person to introduce the concept of electric field. A field can be:
- Any quantity that can be given a value at all points in space around the source of the field; or
- A “region of influence”.
How Electric Fields Work?
First of all, the strength of the electric field is a vector quantity, having a magnitude and a direction. The direction of the field at a point is actually the same direction as the force acting on a positive charge placed at that point.

Let’s say there is a positive point charge, denoted by capital Q. In order to see the effect this charge has on other charges, we’ll bring in its sphere of influence a small positive test charge, denoted by q.
The reason we bring in a small test charge is because we want a value that is independent of the size of the test charge, and depends only on the field’s source and the distance from that source.
Test charge is always positive by definition. Both charges create electric fields, but big Q has a much larger magnitude than small q. The point charge Q modifies the space around it and sets up an electric field.
Electric Field Formula
Now we can measure the field.
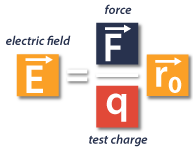
The electric field generated by a charged object, is in fact the electric force between the object and the test charge, divided by the magnitude of that test charge. Coulomb’s Law will help us find the force.
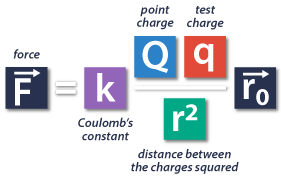
So, in place of capital F, we’ll use the Coulomb’s Law equation.
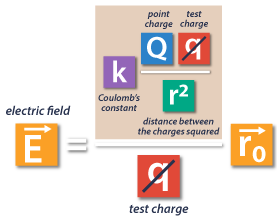
Here, we can notice that small q appears twice in this equation, so it cancels out, and we get an equation that includes only the point charge.

Finally, the strength of an electric field created by a point charge is equal to the Coulomb’s constant multiplied by the charge on the object generating the field, divided by the distance between this object and the test charge squared.
Here we have positive point charge and positive test charge, and the result has a positive sign, meaning that the positively charged object will repel the positive test charge. That’s why the electric field diagram has arrows pointing outward.
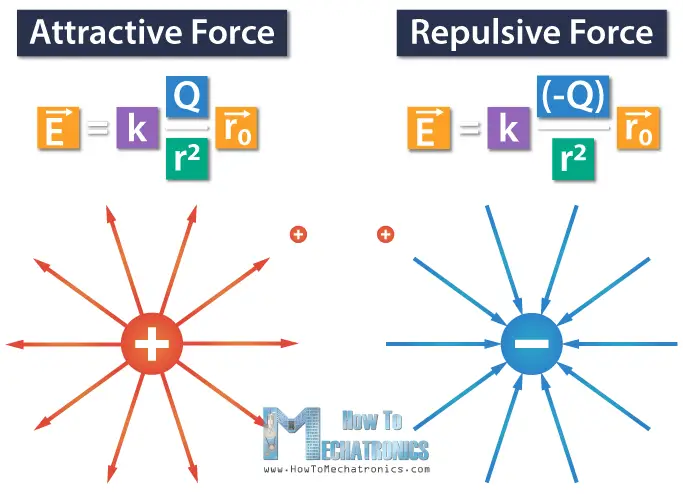
For negative point charge, and positive test charge we have an attractive force, which is shown by the negative sign in the equation.
The electric field line diagram for negatively charged object would look like that of a positively charged object, but with the arrows pointing inward, which means that the negatively charged object Q would attract the positive test charges.
The unit of measurement for electric field is Newtons/Coulomb, or Volts/Meter.
Electric field exists even if there is no test charge nearby to measure it. Similarly, a gravitational field surrounds the earth, even if there is no “test mass” nearby to measure it.

If we know the value of the point charge and the value of the strength of the electric field, we can easily calculate the force, simply by multiplying those values.
Example
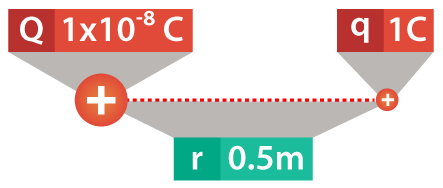
For example, we have a point charge Q equal to 1×10-8 Coulombs. Also, we have a test charge of 1 Coulomb at a 50 cm distance. So, what is the electric field 50 cm away from the point charge?

The electric field at that point is going to be Coulomb’s constant multiplied by the charge generating the field, divided by the distance between the point charge and the test charge squared. This is equal to 9×109 Nm2/C2 times 1×10-8 C divided by (0.5m)2.
Here we can cancel out meters and Coulombs, which gives us Newtons/Coulomb. This is equal to 90 divided by 0.25 Newtons/Coulomb. Finally, the magnitude of the electric field that the point charge generated at 50 cm distance is 360 Newtons/Coulomb.

The force exerted on the test charge is going to be equal to the test charge multiplied by the magnitude of the electric field, which is 1 Coulomb multiplied by 360 Newtons/Coulomb. Here, the Coulombs cancel out, and the force exerted on that 1 Coulomb of charge is going to be 360 Newtons.
Here we can notice that both the point charge and the test charge are positive, so the force will be repulsive, meaning that the direction of the force will be outwards.
Superposition Principle
Superposition principle applies to electric fields as well.
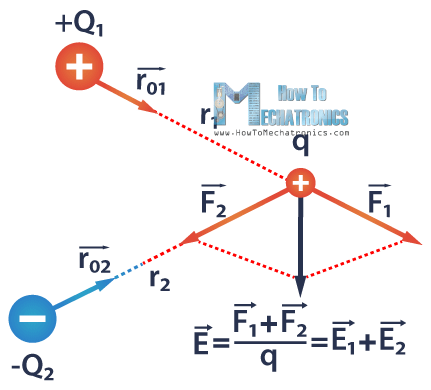
Let’s say we have two point charges Q1 and Q2, and we bring a positive test charge q nearby. Q1 is positive, and Q2 is negative charge. The force that Q1 applies on q is repulsive, and the force that Q2 applies on q is attractive.
The superposition principle can help us calculate the total electric field created by multiple point charges, which is simply a sum of all the individual fields.
In other words, the total electric field at a point from a system of charges acting on a test charge is equal to the vector sum of the electric fields at that point from each of the individual charges.
Using the equation, we can calculate the total electric field E, which is equal to E1 + E2:
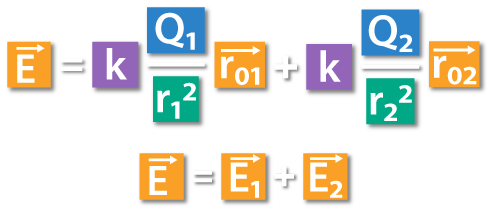
Electric Field Lines
A small positive test charge q placed at various points near Q would be repelled (or attracted) by Q and would move along the lines. These vectors are called lines of force, or electric field lines, a concept first introduced by Michael Faraday.

They show the direction and the magnitude of the force applied on any nearby positive test charge. It is actually the direction that a mobile positive charge would move if placed in the field.
Properties of Electric Field Lines
Let’s take a look at the field between two charges of similar magnitude but opposite sign. They form an electric dipole.
Now let’s connect their electric fields and create a total electric field.
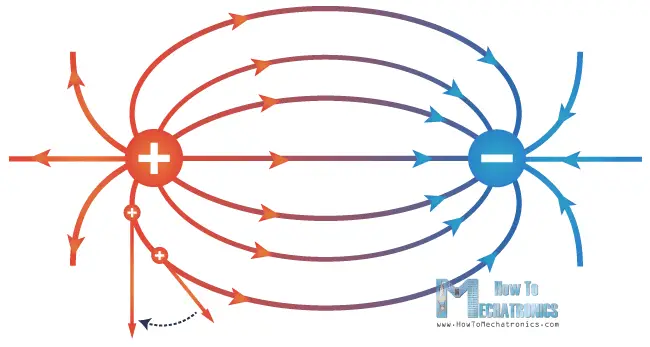
If we pay attention to this total electric field it will reveal four important properties of electric field lines.
- The lines always begin on positive charges and end on negative charges. In our example the lines start at the positively charged object and move toward the negatively charged one. The same number of lines come out of each particle because the magnitude of their charges is equal and opposite.
- The field lines must be tangent to the direction of the field at any point.
- The closeness of the lines indicates the strength of the field. The greater the line density, the greater the magnitude of the field, and opposite.
- The lines never cross. A charge cannot go in two directions at the same time.
OK, that’s all for this tutorial. I hope you enjoyed it and learned something new. In the next Basic Electronics tutorial we will talk about Work and Potential.