In this lecture we will learn about Coulomb’s Law and we will take a look at some simple examples. You can watch the following video or read the written tutorial below.
This law was first defined by French physicist Charles Augustin de Coulomb in 1785 and was essential to the development of the theory of electromagnetism.
Definition of Coulomb’s Law
Coulomb’s Law is a law of physics that describes the interaction between electrically charged objects. It quantifies the amount of electrostatic force that two charged objects exert on each other, which causes an attraction or repulsion between them.
Like charges, for example two positive or two negative charges will repel one another, and unlike charges, one positive and one negative charge will attract one another because of the electrostatic force.
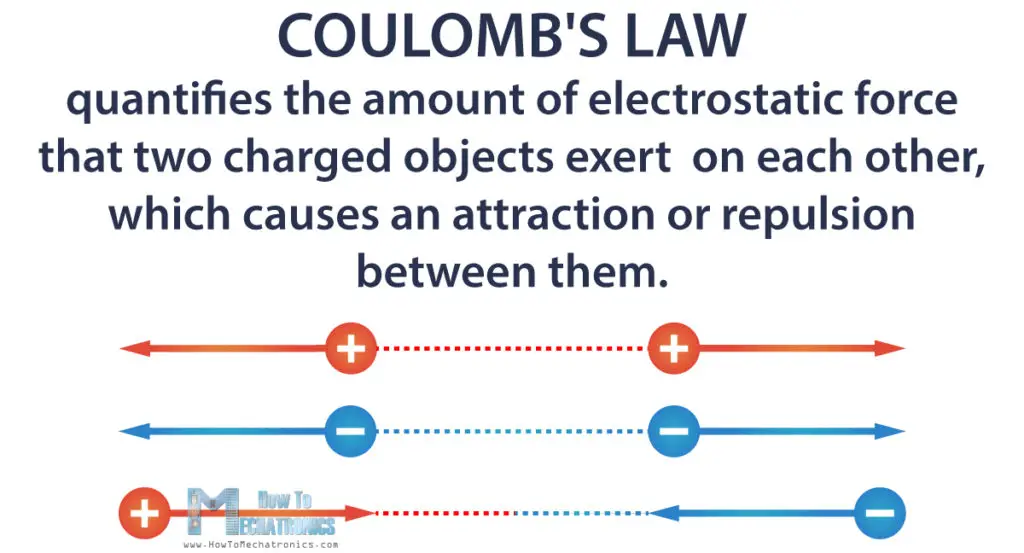
Specifically, this law applies to point charges. Any objects can be treated as point charges, as long as they are very small compared to the distance between them.
Also, the force is along the straight line joining those charges.
Coulomb’s Law Formula
We already know how to measure electric charge. This can help us calculate the electric force between charged objects.
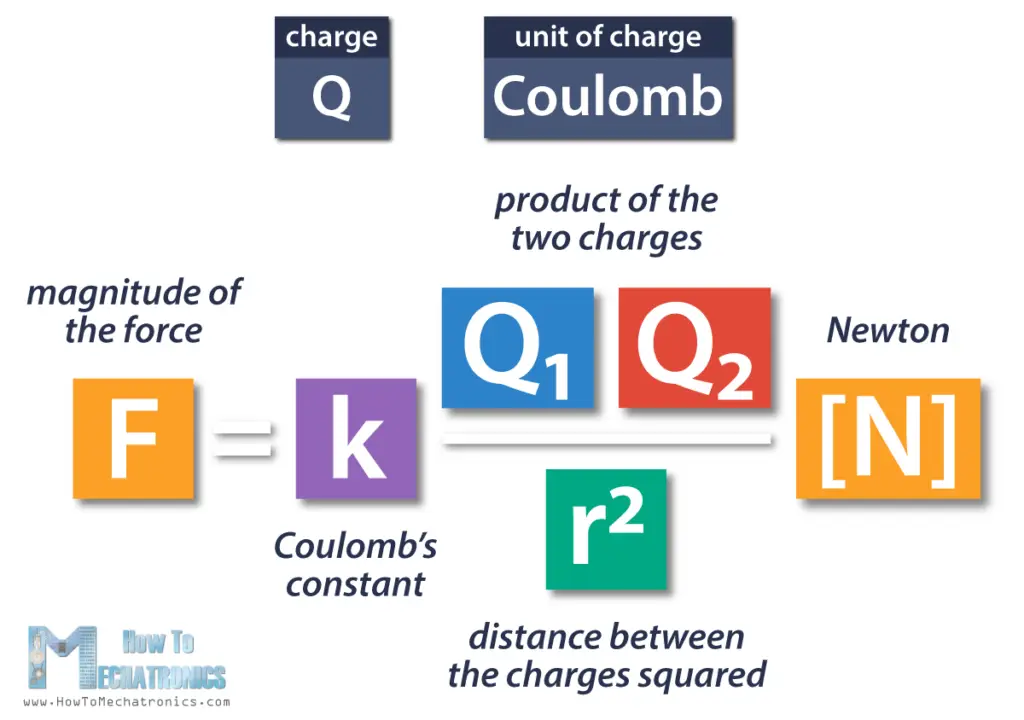
So, the equation shows that the magnitude of the electric force between two charged particles F is equal to the product of the two charges Q1 and Q2, divided by the square of the distance between them r, and all that multiplied by the proportionality constant k.
The electric force is expressed using the unit Newton.
The reason why the distance is squared is because when the distance between objects doubles, the force between them reduces to a quarter of the original value.

In other words, the electric force between two objects increases as the distance between them decreases, and opposite, the force decreases as the distance increases.
The lower-case k is called proportionality constant, or Coulomb’s Law constant. The value of this constant is dependent upon the medium in which the two objects reside. In this case the medium is air.
ε0 is called dielectric constant or vacuum permittivity.
Coulomb’s Law vs Universal Law of Gravitation
If we compare Coulomb’s Law to the Universal Law of Gravitation, we can notice that they have some similarities, but they work in completely different ways.
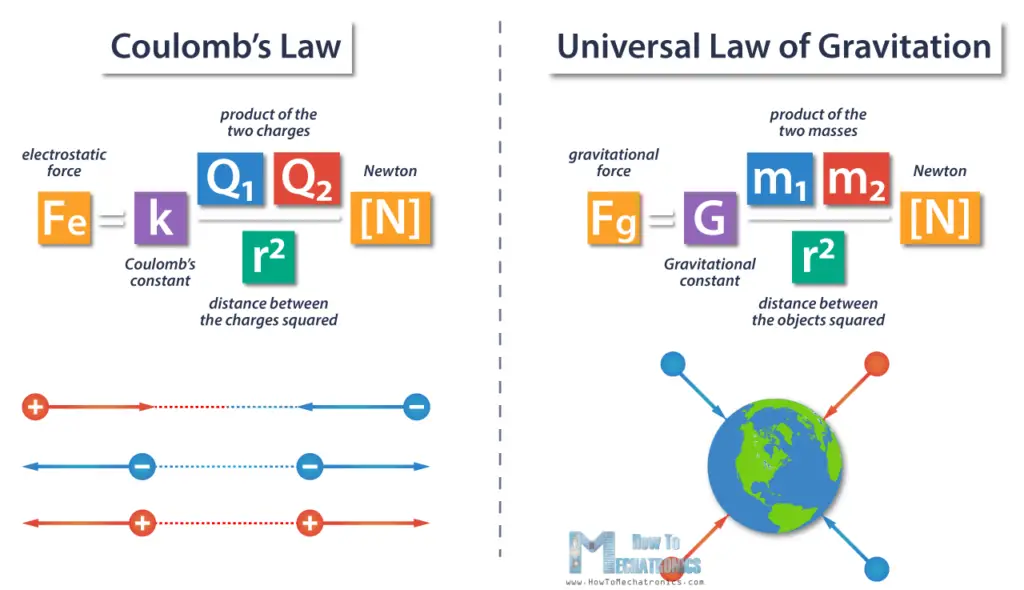
- The electric force is much stronger than gravity.
- From the equations we can notice that they have different proportionality constants.
- In the equation for gravity, we’re using mass to find the force, but in the Coulomb’s Law equation, we’re using charge to find the force.
- Thus, the gravitational force is always attractive, depending on the mass of the objects which is always positive, and on the other side, electrostatic forces can be either attractive or repulsive, depending on the charges, so the result can be negative or positive, respectively.
To sum up, Coulomb’s law states:
- First, the force between two like point charges is repulsive, and between two unlike point charges is attractive;
- Second, the force direction is determined by the line that passes through both charges;
- Third, the magnitude of the force is directly proportional to the product of the two charges, and inversely proportional to the square of the distance between the charges.
Electrostatic Force as a Vector Quantity
Being a force, the strength of the electrical interaction is a vector quantity that has both magnitude and direction. This means that we can calculate the magnitude and the direction of the electric force based on the sign of the result.
Let’s modify the equation.

The arrows in the equation represent a vector quantity.
This is a unit vector pointing from Q1 to Q2, and the index 12 means that Q1 exerts force onto q2.
If we get a positive value, it means that the direction of the force is repulsive. On the other side, the minus sign means that the direction of the force is opposite, or attractive.
Example
Let’s say, we have two positive charges. The first charge Q1 is 2×10-2 C, and the other charge Q2 is 1×10-3C. The distance between them r is 1mm, which is 1×10-3m. Now, we can calculate the force between these charges using the equation.
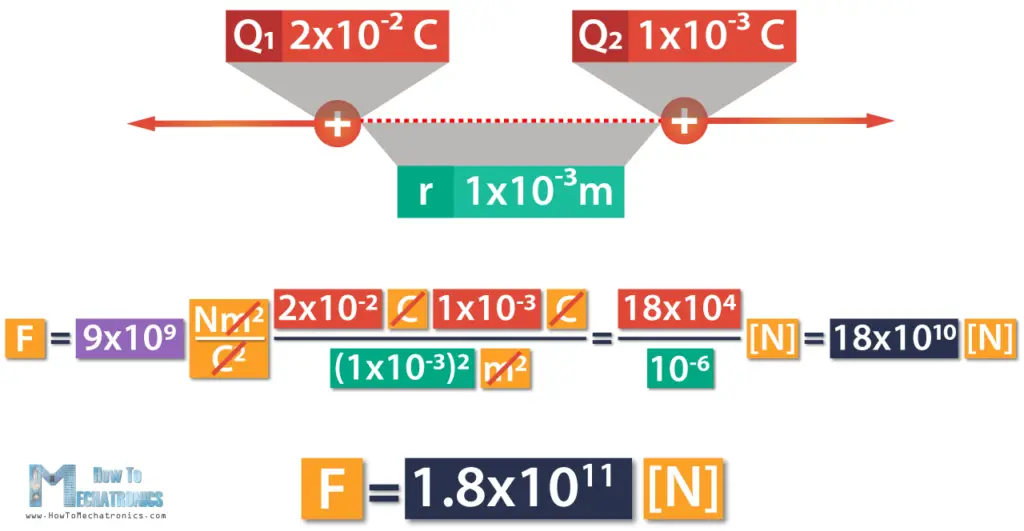
Here we can cancel out meters and Coulombs, which means we’re left with Newtons.
This is equal to 18×104 divided by 10-6, which is 18×1010.
Finally, the force is 1.8×1011 Newtons.
We got a positive result, meaning that the charges repel one another. In case we had one positive and one negative charge, we’d get a negative result, which means they’d attract one another.
Superposition Principle
If there are multiple point charges, let’s say three, we can calculate the force of the two charges that acts on the third charge.
This leads us to the superposition principle which states that for all linear forces the total force is a vector sum of individual forces. This allows Coulomb’s law to be extended to include any number of point charges.
In other words, the total Coulomb force from a system of point charges acting on a point charge, can be found by adding up the forces from each of the other individual charges.
Example
We have three point charges Q1, Q2, and Q, and we need to find the force that Q1 and Q2 exert on Q. Q and Q1 are positive charges, and Q2 is negative charge. The force that Q1 applies on Q, F1 is repulsive, and the force that Q2 applies on Q, F2, is attractive.
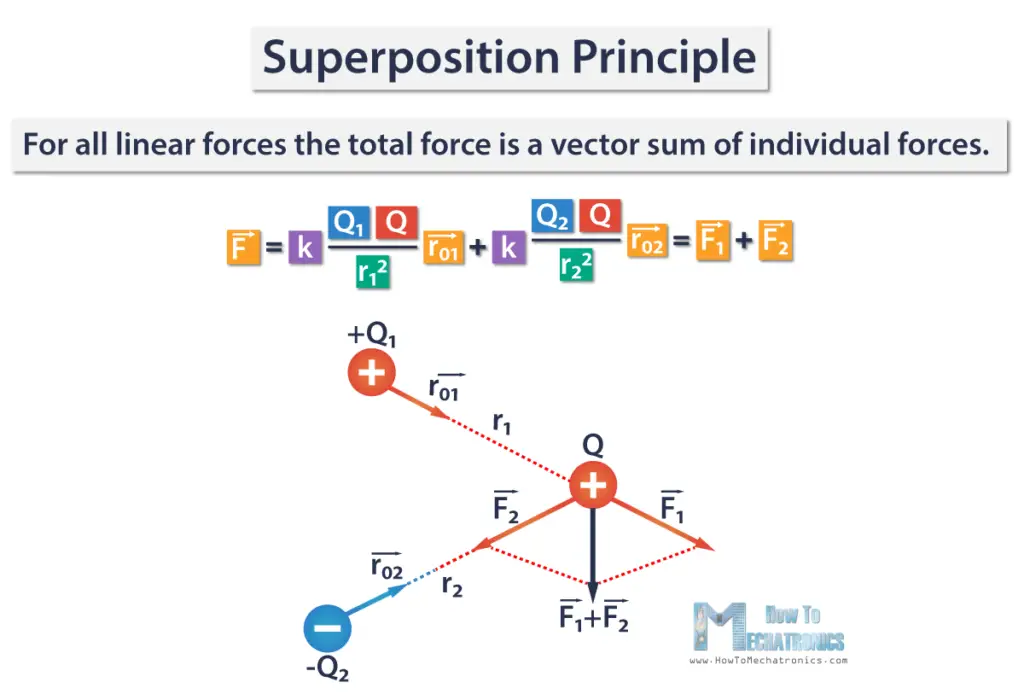
The total electric force F is a sum of the two forces F1 and F2, and is represented with this vector F1+F2.
That’s all for this tutorial. I hope it was helpful and you learned something new. In the next Basic Electronics tutorial we will talk about Electric Fields.