In this lecture we will learn about Electric Flux and Gauss’s Law. In electrostatics, the primary goal of Gauss’s law is to find the electric field for a given charge distribution, enclosed by a closed surface.
You can watch the following video or read the written tutorial below the video.
Electric Flux
In order to understand Gauss’s Law, first we need to understand the term Electric flux.
Electric flux is the rate of flow of the electric field through a given surface.
It is the amount of electric field penetrating a surface. And that surface can be open or closed.
Electric Flux through Open Surfaces
First, we’ll take a look at an example for electric flux through an open surface.
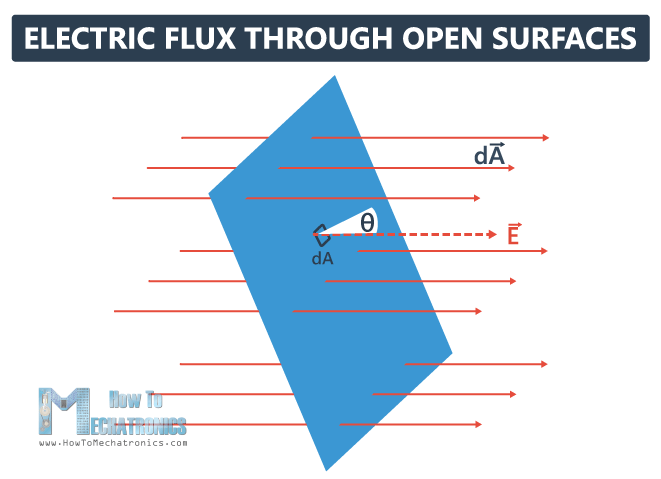
The red lines represent a uniform electric field. We will bring in that field a rectangle, which is an open area, and we will divide it into very small elements, each with size dA (differential of area).
Now we’re going to make the area dA a vector, with a magnitude dA. The vector direction is always perpendicular to the small element dA.
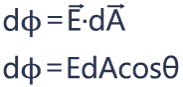
The electric flux that passes through this small area dφ, (also called a differential of flux), is defined as a dot product of the magnitude of the electric field E and the magnitude of the vector area dA, times the angle between these two vectors θ.
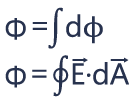
The total flux is going to be the integral of dφ, or the integral over that entire area of E·dA.
It is a scalar quantity and the end result can be positive or negative. If the flux is going from the inside to the outside, we call that a positive flux, if it is going from the outside to the inside, that’s a negative flux.
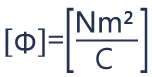
The unit of electric flux is Newton meters squared per Coulomb (Nm2/C).
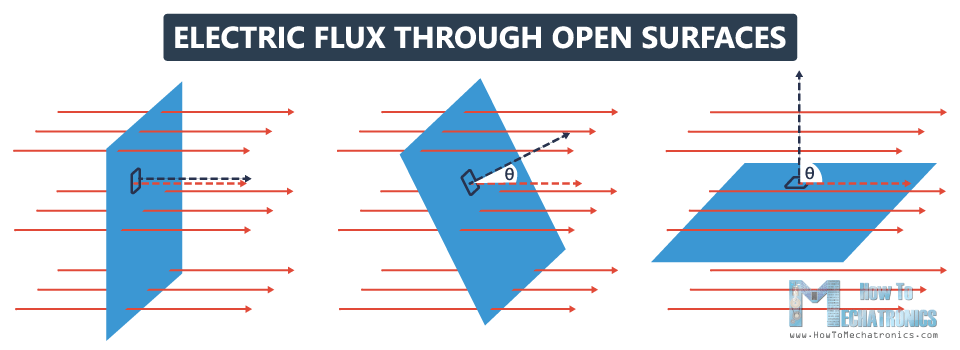
To get a better understanding of what electric flux is, I’ll bring into this electric field three rectangles. In fact, these rectangles represent one rectangle with different orientations. Now let’s explain the flux through each one of those open areas.
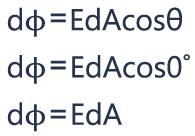
In the first case, the area is perpendicular to the electric field, and the angle between their vectors θ is 0°. Cos0° is 1, so the electric flux is going to be EdA. Here we have maximum flux.
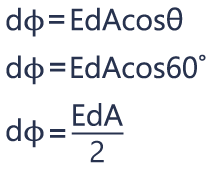
In the second case, the angle between E and dA θ is 60°, and cos60° is 0.5, so the electric flux will be half EdA.
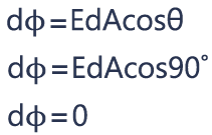
In the third case, the area is parallel to the electric field, which means that their vectors are perpendicular to each other, and the angle θ between them is 90°. Cos90° is 0, so the electric flux here will be 0. This means that nothing goes through that rectangle, so her we have zero flux.
Related: Coulomb’s Law
Electric Flux through Closed Surfaces
Now, let’s take a look at a surface that is completely closed.
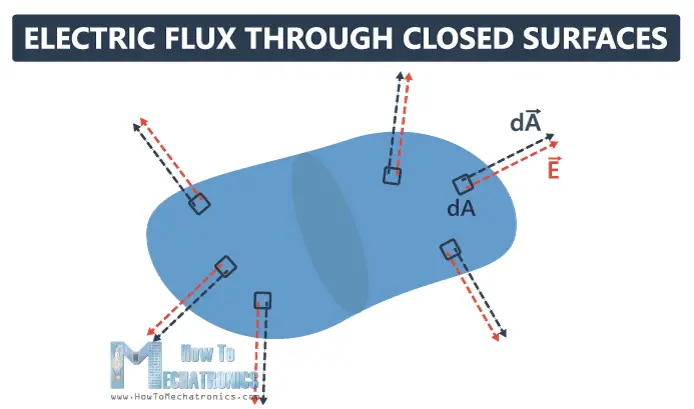
How do we define flux?
Here, we put some normals, dAs in different directions. By convention, the normal to the closed surface always points from the inside to the outside.
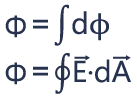
Now we can calculate the total flux going through this closed surface. The total flux is equal to the integral of dφ over that entire surface, which we write as the integral over that closed surface of E·dA.
The total flux can be positive, negative, or equal to zero. If the same amount of flux is entering and leaving the surface, we have zero total flux. If more flux is leaving than entering the surface, then we have positive total flux. Opposite, if more flux is entering than leaving the surface, we have a negative total flux.
Gauss’s Law
Let’s take a look at another example, and see how the electric flux is related to Gauss’s Law.
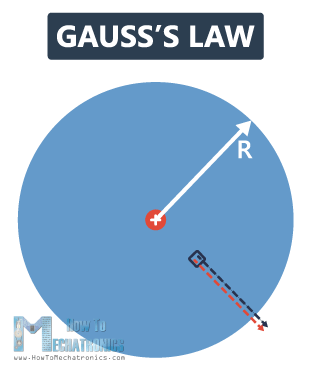
We have a point charge +Q in the center of a sphere with radius R. Now, we’ll take a small segment dA, which vector is perpendicular to the surface and is radially outward. The electric field generated by Q at that point is also radially outward. This means that dA and E anywhere on the surface of this sphere are parallel to each other, the angle between them θ is 0°, and cos0° is 1.

The differential of flux through the small surface area, dφ is equal to EdA.

The total flux Φ is going to be the integral of dφ, which is the integral over the closed surface EdA. The magnitude of the electric field everywhere is the same, because the distance from the charge is the same at each point, so we can pull that out of the integral, and we’re left with EA.

The total area of the sphere A is 4πR2.
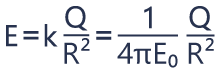
From the previous videos we know that E is equal to k times Q divided by r2, which is equal to Q divided by 4πE0R2.
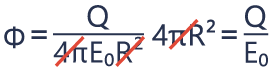
And the total flux through this closed surface is simply E times 4πR2. Here we can cancel out 4πR2, and we can notice that the total flux is equal to Q divided by E0, where E0 is permittivity of free space.
The flux doesn’t depend on the distance r. We would get the same result no matter the size of the closed surface around the point charge.
What if we bring more charges inside the closed surface?
The equation should also hold for any system of charges inside.

This leads us to the Gauss’s Law, which says that the electric flux going through a closed surface, is the sum of all charges Q inside that closed surface, divided by permittivity of free space E0.
If that flux is zero, that means there is no net charge inside the shape. There could be positive and negative charges inside the shape, but the net is zero.
No matter how weird the shape, Gauss’s Law always holds, as long as there’s a symmetry in the charge distribution inside the surface.
So, in order to calculate the electric field, you need a symmetry. And there are three types of symmetry: spherical, cylindrical and planar symmetry.
Related: What is Electric Charge and How Electricity Works
Spherical Symmetry: Electric Field due to a Point Charge
We will start with spherical symmetry.
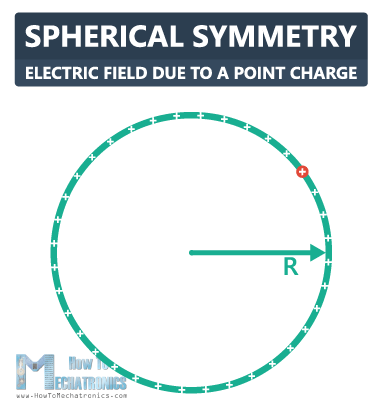
This is a thin hollow sphere, with a radius R, and we’ll bring a positive charge Q onto the thin shell. The charge is uniformly distributed.
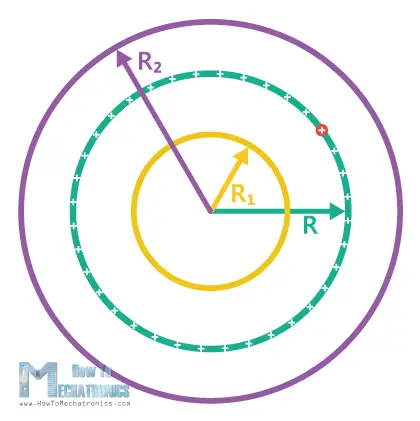
Now, we need to find the electric field inside the sphere, at a distance R1 from the center, and outside the sphere, at a distance R2 from the center. To do that, we need to determine our Gaussian surface. In this case, we will choose concentric spheres as Gaussian surfaces, one smaller with radius R1, and other larger with radius R2.
Now we need to use two symmetry arguments that will help us calculate the electric field:
- The first symmetry argument shows that the magnitude of the electric field is the same at any point, since the charge here is uniformly distributed.
- The second symmetry argument shows that if there is an electric field, it must point either radially outwards, or radially inwards. In this example we have a positive charge, which means the field is pointing outwards.

From the previous equations, we know that the surface area of the sphere, which is 4πr2, times the magnitude of the electric field E is equal to the charge inside the sphere Q, divided by the permittivity of free space E0. But we don’t have a charge inside the smaller sphere, so the electric field is zero.
If a closed surface has no net charge enclosed by it, then the net flux through it will be zero.
Now, let’s see what happens with the larger sphere.
The symmetry arguments hold for this sphere as well. But if we take a look at the equation, we’ll notice that Q is not zero, there’s charge inside that sphere.

So, the magnitude of the electric field will be equal to the Qenclosed divided by 4πE0R22.
Graph for Spherical Symmetry
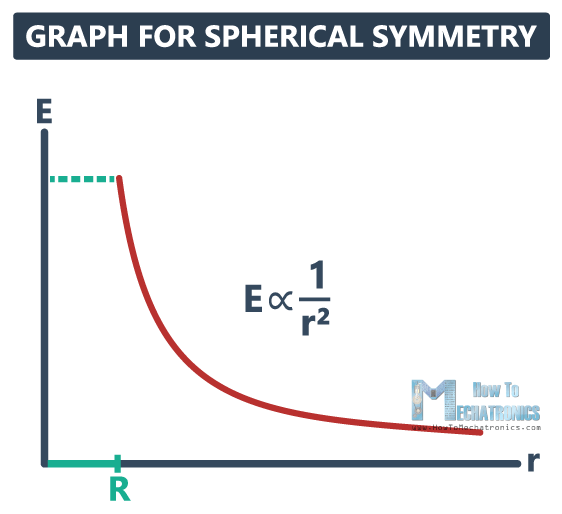
On this graph we have the distance r on the x-axis, and the magnitude of the electric field E on the y-axis. Up to the point R, which is the radius of our initial sphere, we have no electric field, but then it reaches its maximum value, and decreases as the distance increases.
Related: Work and Electric Potential Energy
Cylindrical Symmetry: Electric Field due to a Line of Charge
The second type of symmetry is cylindrical symmetry.
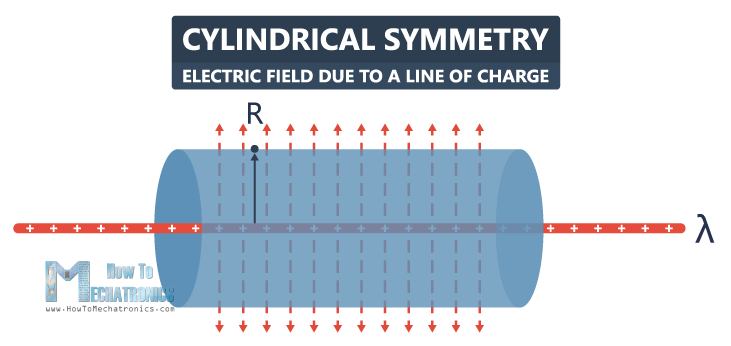
Let’s say we have an infinite line of positive charge, with uniform linear charge density λ, and we want to figure out what the electric field is at some point above the line, at distance R. Here, we’ll choose a cylinder as a Gaussian surface with a center along the line of charge. We don’t have an electric field through the end caps, the electric field will be pointing out through the wall of the cylinder. Also, we have symmetry here, which allows us to use Gauss’s law in order to calculate the electric field.

We can calculate the flux using the same equation that we used previously. But now, we need to find the surface area of the cylinder including the wall, without the end caps. For that purpose, we need to cut the cylinder along its length, and we will find out that the area is equal to 2πrL. So, 2πRL times E is equal to the charge enclosed divided by E0.

The charge density λ is the total charge Q per length L, so the Qenclosed is equal to λL. So, 2πRLE is equal to λL divided by E0.

The electric field is equal to λL divided by 2πRLE0. L cancels out, so the electric field is equal to λ divided by 2πRE0.
Planar Symmetry: Electric Field due to an Infinite Plate
The last type of symmetry is planar symmetry.
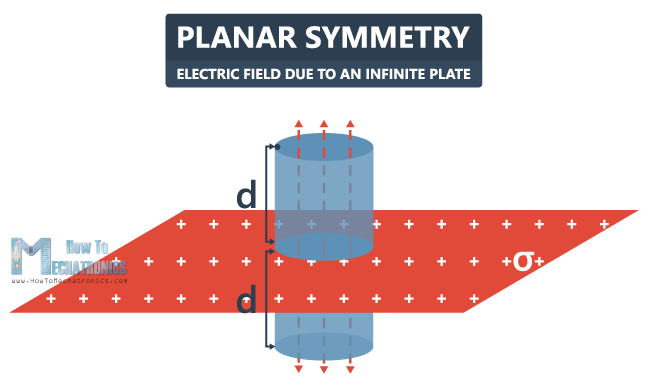
In this example we have a flat, infinitely large horizontal plate. We’ll bring a charge onto this plate, with a uniform charge density σ.
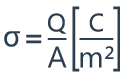
σ is actually an amount of charge per area, expressed in Coulombs per square meter (C/m2).
Now, we want to calculate the electric field in the surrounding area of this plate, let’s say at a distance d. In this case we’re going to choose a cylinder again as a Gaussian surface. The cylinder intersects the plate, and in that intersection we have the charge enclosed.
In order to be able to calculate the electric field, we need to meet three conditions:
- First, the cylinder end caps, with an area A, must be parallel to the plate.
- Second, the walls of the cylinder must be perpendicular to the plate.
- Third, the distance from the plate to the end caps d, must be the same above and below the plate.
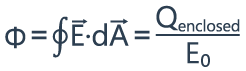
Now that we meet the symmetry requirements, we can calculate the electric field using the Gauss’s law. We’re not going to have any horizontal component of electric field, only vertical, coming out of the two end caps.
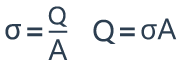
σ is equal to the charge divided by the surface. From this equation we can see that the charge Q is equal to σ times the area A.
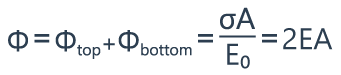
The flux from the wall of the cylinder is equal to zero, so the total flux consists of two components: the flux through the top cap plus the flux through the bottom cap of the cylinder. This is equal to Qenclosed divided by E0, or σA divided by E0. But also the flux through the top, and the flux through the bottom can be expressed as EA, so the total flux is equal to 2EA.

Finally, the electric field is equal to sigma divided by 2E0.
If the plate is positively charged, the electric field would be pointing outwards. If the plate is negatively charged, the electric field would be pointing inwards.
Graph for Planar Symmetry
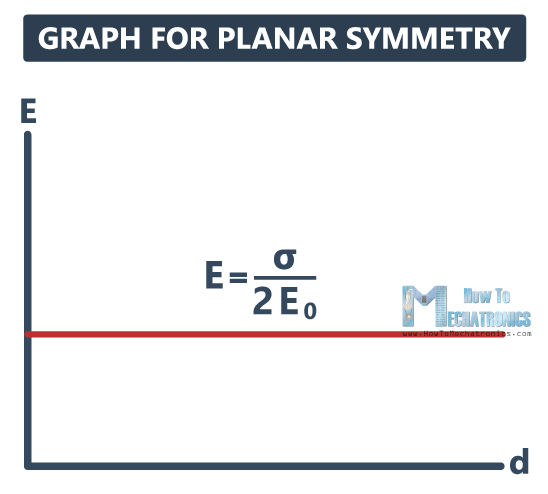
If we draw a graph with the distance d on the x-axis, and the electric field E on the y-axis, we will notice that the electric field has a constant value of σ/2E0, and it doesn’t depend on the distance from the plane.
Related: Electric Potential and Electric Potential Difference (Voltage)
Planar Symmetry: Electric Field due to Two Parallel Plates
Now let’s take a look at another more complex situation of two infinitely large parallel plates.
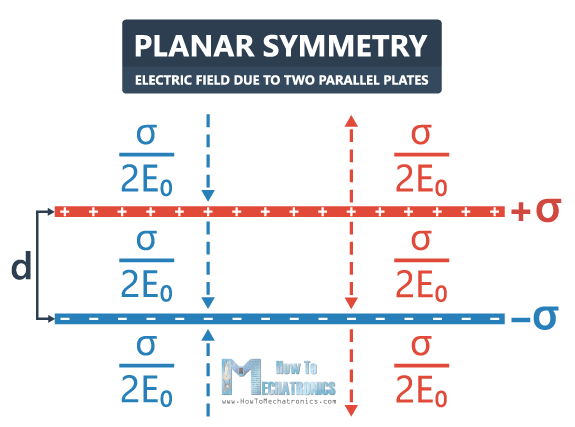
The first plate has a surface charge density +σ, and the plate below has a surface charge density -σ. The distance between them is d.
So, what is the electric field anywhere is space?
The positively charged plate has an electric field pointing away from the plate, equal to σ/2E0. It doesn’t depend on the distance from the plate, so it continues below.
The negatively charged plate has an electric field pointing towards the plate, also equal to σ/2E0.
In order to calculate the total electric field, we’re going to use the superposition principle by adding the vectors.
The vectors that are in the opposite direction cancel out, so the electric field there is zero. The vectors between the plates are in the same direction, so the electric field is σ/E0.
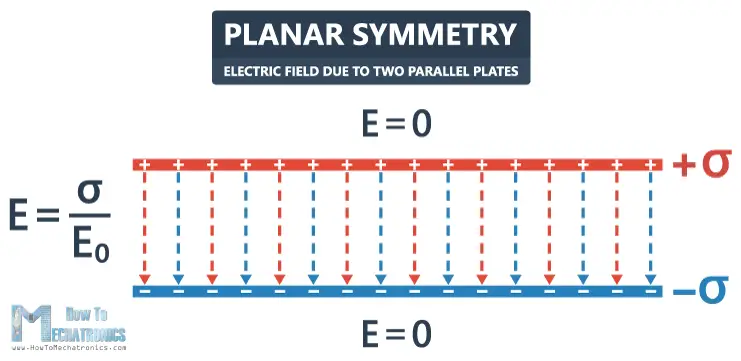
The electric field lines will be pointing away from the positively charged plate and towards the negatively charged plate, and the electric field outside will be zero.
That’s all for electric flux and Gauss’s Law. I hope you enjoyed this tutorial and learned something new. Feel free to ask any question in the comments section below.
good for student and good explain